I've spent most of the past two months implementing planning and curiosity, running experiments, and writing my thesis. The title of it is "Design and Implementation of General Purpose Reinforcement Learning Agents." I put a link to the pdf version on my website here: http://www.vrac.iastate.edu/~streeter. It sums up most of my ideas over the past year or so, including some new ones since my last post.
By the way, I have a working version of the Verve library ready. I just need to clean up a few things before releasing it. As soon as someone bugs me about it, I'll hurry up and get it ready.
Monday, December 12, 2005
Tuesday, October 18, 2005
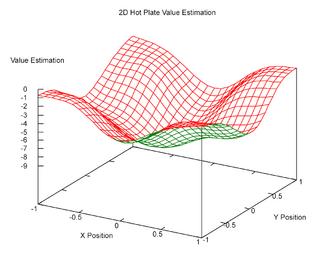
One more value function image...
Monday, October 17, 2005
Simple value function images
Here are a couple of sample (estimated) value functions, both using radial basis functions for state representation.
The first one is for an agent in a 1D world with -1 reward everywhere except on the left and right side:

This second one is for an agent in a 2D world with -1 reward everywhere except at the 4 corners:

The first one is for an agent in a 1D world with -1 reward everywhere except on the left and right side:

This second one is for an agent in a 2D world with -1 reward everywhere except at the 4 corners:

State representation update
I've been working on writing my master's thesis lately. I'm trying to finish it by Nov. 1st. I'll post a link to it when I'm done. I also plan on overhauling the Verve website before too long... at least by the time I release an initial version.
Here's a quick summary of my recent thoughts on state representation:
The main changes when replacing the boxes with RBFs are the following: Instead of using a state-action array of boxes, we need an "observation"-action array of RBFs. Here we are taking the actual sensory input (i.e. the observation) combined with a particular action and transforming them into an RBF representation. This RBF array projects to a predicted observation and reward array of neurons. The system is still trained using a delta rule. The observation/reward predictor no longer uses a winner-take-all rule: instead of choosing a single next state, we have an array of real-valued outputs representing the predicted next observation (and reward).
More to come when I get further...
Here's a quick summary of my recent thoughts on state representation:
- The agent should have a linear state representation in order to assure temporal difference learning convergence. We need to transform the direct sensory inputs into this linear form.
- The state representation should contain features that combine certain inputs where necessary. For a general purpose agent we need to use features that encompass all possible combinations of sensory inputs. Over time the features that never get used could be purged.
- The boxes approach, tile coding, radial basis functions, etc. are all valid methods we could use to represent these features in a linear form. For now I'm choosing an RBF state representation that combines all inputs. Later I would like to experiment with hierarchies of RBF arrays to mimic the hierarchical sensory processing in the cortex.
- We could reduce the dimensionality of sensory inputs by using principal components analysis (PCA) or independent components analysis (ICA). I considered trying this, but I won't have time before finishing my thesis. I might use the "candid covariance-free incremental principal component analysis" (CCIPCA) method since it's incremental and seems fast.
The main changes when replacing the boxes with RBFs are the following: Instead of using a state-action array of boxes, we need an "observation"-action array of RBFs. Here we are taking the actual sensory input (i.e. the observation) combined with a particular action and transforming them into an RBF representation. This RBF array projects to a predicted observation and reward array of neurons. The system is still trained using a delta rule. The observation/reward predictor no longer uses a winner-take-all rule: instead of choosing a single next state, we have an array of real-valued outputs representing the predicted next observation (and reward).
More to come when I get further...
Tuesday, September 20, 2005
I Need a Better State Representation
I'm trying to come up with a better way to represent the current state. Right now I use the "boxes" approach, as described in the last post. Another idea is "tile coding" (aka CMAC) described in Sutton & Barto's RL book. I think the boxes method is like having a single tiling, but in general you could have any number of tilings, each offset a little from the others. That means that with 5 tilings over some input space, you would have 5 active tiles, one from each tiling. Tile coding would give better generalization than using the simple boxes approach. Also, there are ways to use hashing to reduce the memory needed; memory would only be allocated when new states are encountered.
It would be nice to have an array of states where only the "important" states are represented. This could even be dynamic where newly encountered states are compared to the existing list of states. If a new state is different enough, it would be added to the list.
There are a lot of things I could try, but I want to finish adding new features and testing before October, then write my thesis in November. So if I'm going to improve the state representation, I don't want to have to try anything too experimental.
It would be nice to have an array of states where only the "important" states are represented. This could even be dynamic where newly encountered states are compared to the existing list of states. If a new state is different enough, it would be added to the list.
There are a lot of things I could try, but I want to finish adding new features and testing before October, then write my thesis in November. So if I'm going to improve the state representation, I don't want to have to try anything too experimental.
Tuesday, September 13, 2005
Solved Pendulum Task (and others)
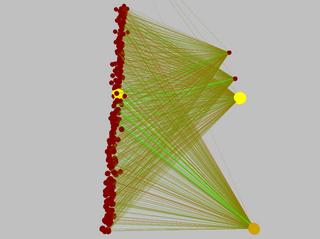
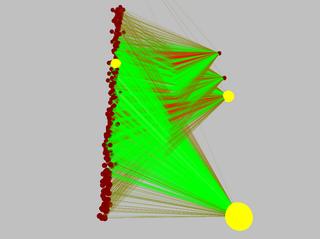
I finally solved the pendulum swing-up task the other day. Here's a picture of it balancing itself:

The main change that helped solve this task was the following relatively major change: I no longer use radial basis functions. Instead, I discretize all incoming continuous inputs into separate "boxes" (to use the terminology from the literature) and generate a list of all possible combinations of the input signals. So in the case of the pendulum, say we discretize the two inputs (pendulum angle and angular velocity) into 12 boxes each. That means the intermediate state representation is an array of 144 possible combinations, each one representing a unique state. It's kind of a brute-force method, but it's very reliable and easy to understand. I may come back to radial basis functions and hebbian learning mechanisms later to form a more compact state representation.
Here are some pictures of the pendulum's (simple) neural network before and after learning the task. Excitatory connections are green, inhibitory are red. The connection diameter represents its weight's magnitude.
So here's a list of the tasks solved so far (with the number of inputs and outputs specified as (inputs/outputs)):
- N-armed bandit (0/10)
- hot plate (1/3)
- signaled hot plate (2/3)
- 2D signaled hot plate (3/5)
- pendulum swing up (2/3)
Next up: the inverted pendulum (aka cart-pole)...
One more thing: I used SWIG to generate Python bindings. Verve seems to work pretty well as a Python module. I don't know if I'll use it much right away, but it's good to have around.

The main change that helped solve this task was the following relatively major change: I no longer use radial basis functions. Instead, I discretize all incoming continuous inputs into separate "boxes" (to use the terminology from the literature) and generate a list of all possible combinations of the input signals. So in the case of the pendulum, say we discretize the two inputs (pendulum angle and angular velocity) into 12 boxes each. That means the intermediate state representation is an array of 144 possible combinations, each one representing a unique state. It's kind of a brute-force method, but it's very reliable and easy to understand. I may come back to radial basis functions and hebbian learning mechanisms later to form a more compact state representation.
Here are some pictures of the pendulum's (simple) neural network before and after learning the task. Excitatory connections are green, inhibitory are red. The connection diameter represents its weight's magnitude.


So here's a list of the tasks solved so far (with the number of inputs and outputs specified as (inputs/outputs)):
- N-armed bandit (0/10)
- hot plate (1/3)
- signaled hot plate (2/3)
- 2D signaled hot plate (3/5)
- pendulum swing up (2/3)
Next up: the inverted pendulum (aka cart-pole)...
One more thing: I used SWIG to generate Python bindings. Verve seems to work pretty well as a Python module. I don't know if I'll use it much right away, but it's good to have around.
Saturday, August 06, 2005
Extensive Testing
So what's new over the past 2 months? Mainly, I have been creating lots of different tests (unit tests and "learning tests"). I was on the brink of finishing the pendulum swing-up task... for about two weeks. It gets frustrating after seeing the pendulum almost hold itself up for the 1000th time, so I took a step back and decided to go about things more scientifically. I developed a framework for what I'm calling "learning tests" - simple learning tasks that can be thrown together quickly and added to an ever-growing suite. Every time I make a significant change in how the agent's work, I can run the suite of learning tests and make sure the agents perform each one above some threshold. I also plot the results of each one using gnuplot (http://www.gnuplot.info). Here are a few example plots (green is overall performance, red is temporal difference error):
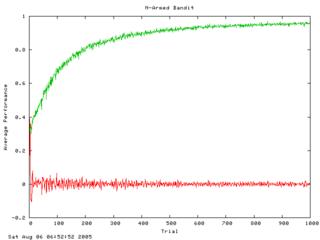
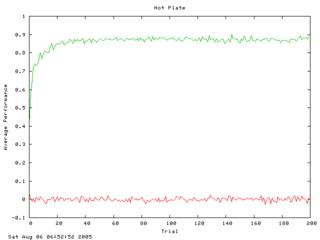
Also, I wrote a bunch of unit tests to make sure each functional component is working correctly even after I make big changes. (I decided to write my own C++ unit testing framework. Check here if you're interested: http://quicktest.sf.net)
The purpose of adding all these tests is so I can scale up the learning task complexity a little at a time and find out exactly where problems occur. This seems much more reasonable than throwing a bunch of complicated systems together (learning agent, physics simulation, etc.) and hope it can learn efficiently.
Another big change has been in the area of input representation. Now the agents' inputs are much more customizeable. You can choose between 'continuous' and 'discrete' input channels. Continuous inputs are real values within [-1, 1]. They have a 'resolution' option which determines how many radial basis functions are used when encoding the input signal as a population code. Discrete inputs have a finite number of possible options. You could have a discrete input channel with 13 possible options representing ace, 2, 3, ..., 9, 10, jack, queen, king. Or you could have one with 2 possible options: alarm on, alarm off.
I'm continually excited about working on this project. It helps my morale to have the unit tests and learning tests. I feel like I can keep making incremental progress this way.
Oh, one more thing... I just bought a new Dell Dimension 9100: dual core 2.8 GHz (to inspire me to make Verve multithreaded :) ), 1 Gb ram, nVidia GeForce 6800, and a 24" LCD.


Also, I wrote a bunch of unit tests to make sure each functional component is working correctly even after I make big changes. (I decided to write my own C++ unit testing framework. Check here if you're interested: http://quicktest.sf.net)
The purpose of adding all these tests is so I can scale up the learning task complexity a little at a time and find out exactly where problems occur. This seems much more reasonable than throwing a bunch of complicated systems together (learning agent, physics simulation, etc.) and hope it can learn efficiently.
Another big change has been in the area of input representation. Now the agents' inputs are much more customizeable. You can choose between 'continuous' and 'discrete' input channels. Continuous inputs are real values within [-1, 1]. They have a 'resolution' option which determines how many radial basis functions are used when encoding the input signal as a population code. Discrete inputs have a finite number of possible options. You could have a discrete input channel with 13 possible options representing ace, 2, 3, ..., 9, 10, jack, queen, king. Or you could have one with 2 possible options: alarm on, alarm off.
I'm continually excited about working on this project. It helps my morale to have the unit tests and learning tests. I feel like I can keep making incremental progress this way.
Oh, one more thing... I just bought a new Dell Dimension 9100: dual core 2.8 GHz (to inspire me to make Verve multithreaded :) ), 1 Gb ram, nVidia GeForce 6800, and a 24" LCD.
Friday, June 17, 2005
Motor Output Representation
Progress has been pretty steady, but slower than I'd like. At least I'm getting close to finishing the pendulum swing up task. Then I can move on to the cart-pole/inverted pendulum task.
My current problem (and probably the last main problem before the pendulum task is finished) is how motor output signals are represented. Here are two possibilities:
1. Use one output neuron for each motor output signal. The neuron's firing rate encodes the motor signal to be used (e.g. a torque value). This allows the use of continuous signals for motor control, a desirable feature. The problem is that any reinforcement (via the temporal difference error) increases or decreases the firing rate of all outputs in the same direction (i.e. all firing rates will either increase or decrease), but we actually might want some to increase and some to decrease. It might be possible to use some kind of differential Hebbian update in conjunction with the temporal difference error (i.e. weight changes are proportional to TD error * pre-synaptic firing rate * change in post-synaptic firing rate), though I haven't read about anyone else doing this.
2. Use a "winner-take-all" scheme to select from among many action choices. Say we have three actions for the pendulum task: apply a constant clockwise torque, apply a constant counter-clockwise torque, or do nothing (letting the pendulum swing freely). Using three output neurons, we choose the one with the highest firing rate as the "winner." The winning neuron's associated action is applied. Another alternative is to have the firing rates represent probabilities of being chosen as the winner. The problem here is that there is a finite number of possible actions. This method currently gives me better results on the pendulum swing up task (it learns to swing the pendulum up and hold it for a second or two), but it can't keep it up indefinitely.
It might be possible (and probably is biologically plausible) to combine the two approaches: fine motor control is learned by one mechanism and encapsulated in a motor program, and another mechanism learns to switch from among a finite set of motor programs. It would be nice to have an agent automatically construct such motor programs, possibly even constructing hierarchies of them. Richard Sutton has done some work recently with what he calls "options" which are basically control policies that have special starting and termination conditions. I think these might be a pretty good theoretical foundation for building hierarchies of motor programs.
My current problem (and probably the last main problem before the pendulum task is finished) is how motor output signals are represented. Here are two possibilities:
1. Use one output neuron for each motor output signal. The neuron's firing rate encodes the motor signal to be used (e.g. a torque value). This allows the use of continuous signals for motor control, a desirable feature. The problem is that any reinforcement (via the temporal difference error) increases or decreases the firing rate of all outputs in the same direction (i.e. all firing rates will either increase or decrease), but we actually might want some to increase and some to decrease. It might be possible to use some kind of differential Hebbian update in conjunction with the temporal difference error (i.e. weight changes are proportional to TD error * pre-synaptic firing rate * change in post-synaptic firing rate), though I haven't read about anyone else doing this.
2. Use a "winner-take-all" scheme to select from among many action choices. Say we have three actions for the pendulum task: apply a constant clockwise torque, apply a constant counter-clockwise torque, or do nothing (letting the pendulum swing freely). Using three output neurons, we choose the one with the highest firing rate as the "winner." The winning neuron's associated action is applied. Another alternative is to have the firing rates represent probabilities of being chosen as the winner. The problem here is that there is a finite number of possible actions. This method currently gives me better results on the pendulum swing up task (it learns to swing the pendulum up and hold it for a second or two), but it can't keep it up indefinitely.
It might be possible (and probably is biologically plausible) to combine the two approaches: fine motor control is learned by one mechanism and encapsulated in a motor program, and another mechanism learns to switch from among a finite set of motor programs. It would be nice to have an agent automatically construct such motor programs, possibly even constructing hierarchies of them. Richard Sutton has done some work recently with what he calls "options" which are basically control policies that have special starting and termination conditions. I think these might be a pretty good theoretical foundation for building hierarchies of motor programs.
Friday, May 27, 2005
Radial Basis Functions, Neural Net Visualization
Two new things...
1. I've been experimenting with a layer of radial basis functions (RBFs) for the input layer to my neural nets. Before I would just use a single real value for each input. For example, the pendulum angle was a single real value which used a single input neuron. Now I separate each input into an array of RBFs. It seems that a lot of people use RBFs when using neural nets for motor control. They increase the "locality" of learning: only the connection weights associated with a particular part of the state space are affected, so it helps the neural net retain old knowledge better. Also, it's neat to think about RBFs in terms of biology (think of the arrays of sensory nerves on the skin, the retina, the vestibular system, etc.)
2. I have always had a hard time visualizing what's going on with the neural networks while they learn. The combination of learning rates, eligibility traces for connections, neuronal firing rates, etc. makes it hard to understand what's going on. I had already been plotting various parameters on graphs after the simulations end, but I really wanted to watch how the parameters change in real time. So I wrote some code to see the neural nets floating in 3D space beside the agent's physical body. It shows me the neuron firing rates, connection weight sign/magnitudes, and eligibility traces, making it much easier to see what's going on.
1. I've been experimenting with a layer of radial basis functions (RBFs) for the input layer to my neural nets. Before I would just use a single real value for each input. For example, the pendulum angle was a single real value which used a single input neuron. Now I separate each input into an array of RBFs. It seems that a lot of people use RBFs when using neural nets for motor control. They increase the "locality" of learning: only the connection weights associated with a particular part of the state space are affected, so it helps the neural net retain old knowledge better. Also, it's neat to think about RBFs in terms of biology (think of the arrays of sensory nerves on the skin, the retina, the vestibular system, etc.)
2. I have always had a hard time visualizing what's going on with the neural networks while they learn. The combination of learning rates, eligibility traces for connections, neuronal firing rates, etc. makes it hard to understand what's going on. I had already been plotting various parameters on graphs after the simulations end, but I really wanted to watch how the parameters change in real time. So I wrote some code to see the neural nets floating in 3D space beside the agent's physical body. It shows me the neuron firing rates, connection weight sign/magnitudes, and eligibility traces, making it much easier to see what's going on.
Friday, May 20, 2005
Fixed Problems with Multilayer Neural Network
I discovered yesterday that it really helps to connect the input neurons directly to the output neurons in the multilayer neural net. Now the value function neural net learns really well. The temporal difference error almost always goes to +/- 0.001 eventually.
Now I'm having trouble with the policy/actor neural net. It doesn't seem to improve its performance very much. It'll learn to swing the pendulum a little higher over time, but it never gets high enough to swing straight up. It definitely has enough torque, so that's not the problem. I wonder if it needs more random exploration. I'm currently using a low-pass filtered noise channel that changes slowly over time to encourage long random actions. I'll keep trying stuff...
Now I'm having trouble with the policy/actor neural net. It doesn't seem to improve its performance very much. It'll learn to swing the pendulum a little higher over time, but it never gets high enough to swing straight up. It definitely has enough torque, so that's not the problem. I wonder if it needs more random exploration. I'm currently using a low-pass filtered noise channel that changes slowly over time to encourage long random actions. I'll keep trying stuff...
Thursday, May 19, 2005
Problems Learning the Value Function with a Multilayer Neural Network
I've noticed that my agents can learn the value function really well using a linear function approximator - a neural network with a single output layer using linear activation functions. However, when I add a hidden layer of neurons, the agent cannot learn the value function very closely (i.e. the temporal difference error fluctuates between -0.1 and +0.1; the max possible error is +/-1.0). I usually use sigmoid activation functions for the hidden neurons, so I tried linear functions for them as well, but it didn't help. So I'm trying to figure out why it can't converge to something closer to the real value function using a hidden and output layer of neurons. I know that there are not any good convergence guarantees for nonlinear function approximators using temporal difference, but I at least thought using linear activation functions in all neurons, even in a multilayer neural network, still represented a linear function approximator. So maybe something else is wrong.
On the other hand, maybe I won't really need a nonlinear function approximator. It seems like a lot of researchers do pretty well with linear only, but then they only attempt fairly simple control problems.
I've learned a good way to represent the state for the pendulum swing up task. I was inputting the sine and cosine of the pendulum's angle (plus the angular velocity), similar to what Remi Coulom did in his thesis, but I had trouble learning the value function with this method, even with a single layer neural network. Instead I tried representing the angle as two inputs: one "turns on" when the pendulum is between 0 and 180 degrees (the input value ranging from 0 to 1) while the other is "off" (i.e. value of 0). When the pendulum is between 180 and 360 degrees, the first input is off and the other is on. This seemed to work really well - the temporal difference error usually falls to around +/-0.001 within a few minutes of real-time training.
On the other hand, maybe I won't really need a nonlinear function approximator. It seems like a lot of researchers do pretty well with linear only, but then they only attempt fairly simple control problems.
I've learned a good way to represent the state for the pendulum swing up task. I was inputting the sine and cosine of the pendulum's angle (plus the angular velocity), similar to what Remi Coulom did in his thesis, but I had trouble learning the value function with this method, even with a single layer neural network. Instead I tried representing the angle as two inputs: one "turns on" when the pendulum is between 0 and 180 degrees (the input value ranging from 0 to 1) while the other is "off" (i.e. value of 0). When the pendulum is between 180 and 360 degrees, the first input is off and the other is on. This seemed to work really well - the temporal difference error usually falls to around +/-0.001 within a few minutes of real-time training.
Thursday, May 12, 2005
More Time for Research
Summer's here, so I finally have time for research again. I'm going to (try to) graduate with a master's degree this summer, so I'll be working on this project a lot over the next few months.
I didn't find any definitive answer concerning time representation in Daw's dissertation, but it was still a great (long) read. I'm still using it as a reference. I implemented some of his ideas about average reward rates (as opposed to discounted rewards, the standard method in temporal difference learning) and opponent dopamine/serotonin channels. The dopamine channel represents phasic (short-term) rewards and tonic (long-term) punishment, and the serotonin channel represents phasic punishment and tonic rewards. Eventually I'd like to do some experiments to see if this model more closely mimics animal behavior.
I've pretty much decided what I'm going to cover in my thesis. The main two topics are 1) temporal difference learning for motor control in continuous time and space, and 2) artificial neural networks for function approximation. My focus is on biologically realistic algorithms, so I'll spend some time talking about how my implementation relates to the brain. I'd like to include at least three experiments with solid results. I'm thinking maybe the pendulum swing up task (a pendulum hanging in midair has to swing itself upright and stay there using a limited amount of torque), the cart-pole task (a cart resting on a plane with an attached pole must force the cart back and forth to keep the pole balanced), and maybe a legged creature that learns to walk.
Another possible addition is the use of a learned model of the environment's dynamics, also using an artificial neural network. We'll see if I have time for that. I'd really like to try it, though, because others (e.g. Doya in his 2000 paper on continuous reinforcement learning) have gotten better results in motor control tasks using a learned dynamics model.
So far I've been working on the pendulum task. I have my value function (critic) working pretty well, but I can't get the policy (actor) to learn very well. I'm thinking my problem is either with my exploration method or how I'm representing the state as inputs to the neural nets.
I didn't find any definitive answer concerning time representation in Daw's dissertation, but it was still a great (long) read. I'm still using it as a reference. I implemented some of his ideas about average reward rates (as opposed to discounted rewards, the standard method in temporal difference learning) and opponent dopamine/serotonin channels. The dopamine channel represents phasic (short-term) rewards and tonic (long-term) punishment, and the serotonin channel represents phasic punishment and tonic rewards. Eventually I'd like to do some experiments to see if this model more closely mimics animal behavior.
I've pretty much decided what I'm going to cover in my thesis. The main two topics are 1) temporal difference learning for motor control in continuous time and space, and 2) artificial neural networks for function approximation. My focus is on biologically realistic algorithms, so I'll spend some time talking about how my implementation relates to the brain. I'd like to include at least three experiments with solid results. I'm thinking maybe the pendulum swing up task (a pendulum hanging in midair has to swing itself upright and stay there using a limited amount of torque), the cart-pole task (a cart resting on a plane with an attached pole must force the cart back and forth to keep the pole balanced), and maybe a legged creature that learns to walk.
Another possible addition is the use of a learned model of the environment's dynamics, also using an artificial neural network. We'll see if I have time for that. I'd really like to try it, though, because others (e.g. Doya in his 2000 paper on continuous reinforcement learning) have gotten better results in motor control tasks using a learned dynamics model.
So far I've been working on the pendulum task. I have my value function (critic) working pretty well, but I can't get the policy (actor) to learn very well. I'm thinking my problem is either with my exploration method or how I'm representing the state as inputs to the neural nets.
Wednesday, February 23, 2005
Time Representation
Last month I mentioned that I was running a classical conditioning experiment on my new agents. Given some stimulus at time t and a reward at time t+ISI (where ISI is a constant "inter-stimulus interval"), the agent should learn to predict when the time and magnitude of the reward after experiencing the stimulus. So, in other words, after the agent has been trained to predict the reward, when it sees the stimulus (which was previously neutral but now predicts reward), it should now exactly how long to wait before getting the reward and how big the reward will be.
My current problem is that the agent doesn't have a good way to represent the passage of time, a crucial element in classical conditioning. The agent can predict rewards immediately following the stimulus, but if there is a significant gap (ISI) between the stimulus and reward, the agent quickly forgets about the stimulus. I think I'm about to find some answer's in Nathaniel Daw's PhD thesis. Daw finished his thesis at Carnegie Mellon in 2003. The title of it is "Reinforcement Learning Models of the Dopamine System and their Behavioral Implications." It contains a lot of good material, including an extensive literature review and some new ideas about long-term reward predictions. Anyway, I'm just getting into chapter 4 which deals with time representation. I'm hoping to find some ideas there.
My current problem is that the agent doesn't have a good way to represent the passage of time, a crucial element in classical conditioning. The agent can predict rewards immediately following the stimulus, but if there is a significant gap (ISI) between the stimulus and reward, the agent quickly forgets about the stimulus. I think I'm about to find some answer's in Nathaniel Daw's PhD thesis. Daw finished his thesis at Carnegie Mellon in 2003. The title of it is "Reinforcement Learning Models of the Dopamine System and their Behavioral Implications." It contains a lot of good material, including an extensive literature review and some new ideas about long-term reward predictions. Anyway, I'm just getting into chapter 4 which deals with time representation. I'm hoping to find some ideas there.
Wednesday, January 19, 2005
Research update
Things are changing.
I have spent the past two months reading literature on two topics:
1) Reinforcement learning (for machines)
2) Reward signals in biological learning systems
A few months ago I started exploring things other than evolutionary methods. I couldn't help thinking that one of the best ways to improve machine learning methods is by studying and mimicking biological brains. At the same time I dove deeper into the (machine) reinforcement learning literature, trying to find out which methods are the best for motor control.
I decided to read the book Reinforcement Learning by Sutton & Barto over Christmas break, something I probably should have read a long time ago. Before reading it, my plan was to try out an actor-critic architecture, along with some kind of "sensory predictor" (a module that could learn to predict future sensory inputs based on some given state and action). The sensory predictor would allow an agent to simulate its environment and make decisions based off those simulations. I was proud of this idea at the time since I had thought of it one day in the middle of class, but later found out it already existed. Also, I had heard something about temporal difference learning methods (from the neuroscientific literature - dopamine neuron behavior is very similar to the temporal difference error signal), but I didn't know much about them. So I read Reinforcement Learning straight through. It turns out that temporal difference learning is a very effective way to predict future rewards (in the critic) AND to modify the actor's policy to reinforce effective actions (using "eligibility traces"). This works even when the reinforcement received from the environment is sparse. Temporal difference methods learn to associate neutral stimuli with rewards, thus creating chains of reward-predicting stimuli. Very cool stuff. And, the more I read in the neuroscientific literature about reward signals in the brain, the more confident I become that biological brains use temporal difference learning.
Additionally, the Reinforcement Learning book made it clear to me why neural networks are important. In the real world there are so many possible states that an agent cannot simply store an internal table of each state or state-action pair, along with reward estimates for each. A neural network condenses the state space by using a small set of parameters to approximate a more complex function.
At this point I have made a fairly permanent switch from evolutionary methods to reinforcement learning methods. I have written a good chunk of code so far to begin testing new ideas, including the basic neural network setup, temporal difference learning, and back-propagation. The back-prop will probably be used by the "sensory predictor" (i.e. internal/world model) to learn an internal representation of the external environment. Back-prop seems to be good for this because there will be predicted sensory inputs and actual sensory inputs, naturally leading to error signals at each output neuron.
I have run a few simple tests to make sure each component is functioning properly. The thing I'm testing now is a simple classical conditioning response. I'm trying to get my new agents to be able to predict rewards given some stimulus 200 ms before reward reception.
In the future I would like to setup a SETI-like system for training simulated creatures and/or robots. I think it would be a good way to get people involved in AI research, not to mention the extra CPU resources.
Right now I'm preparing a Verve presentation for the ISU Robotics Club tomorrow which will basically cover everything in this post, plus a little more background information. I'm hoping to use Verve to train real robots in the future (as opposed to simulated creatures). Maybe some folks from the club will be interested in working on something like that.
Tyler
I have spent the past two months reading literature on two topics:
1) Reinforcement learning (for machines)
2) Reward signals in biological learning systems
A few months ago I started exploring things other than evolutionary methods. I couldn't help thinking that one of the best ways to improve machine learning methods is by studying and mimicking biological brains. At the same time I dove deeper into the (machine) reinforcement learning literature, trying to find out which methods are the best for motor control.
I decided to read the book Reinforcement Learning by Sutton & Barto over Christmas break, something I probably should have read a long time ago. Before reading it, my plan was to try out an actor-critic architecture, along with some kind of "sensory predictor" (a module that could learn to predict future sensory inputs based on some given state and action). The sensory predictor would allow an agent to simulate its environment and make decisions based off those simulations. I was proud of this idea at the time since I had thought of it one day in the middle of class, but later found out it already existed. Also, I had heard something about temporal difference learning methods (from the neuroscientific literature - dopamine neuron behavior is very similar to the temporal difference error signal), but I didn't know much about them. So I read Reinforcement Learning straight through. It turns out that temporal difference learning is a very effective way to predict future rewards (in the critic) AND to modify the actor's policy to reinforce effective actions (using "eligibility traces"). This works even when the reinforcement received from the environment is sparse. Temporal difference methods learn to associate neutral stimuli with rewards, thus creating chains of reward-predicting stimuli. Very cool stuff. And, the more I read in the neuroscientific literature about reward signals in the brain, the more confident I become that biological brains use temporal difference learning.
Additionally, the Reinforcement Learning book made it clear to me why neural networks are important. In the real world there are so many possible states that an agent cannot simply store an internal table of each state or state-action pair, along with reward estimates for each. A neural network condenses the state space by using a small set of parameters to approximate a more complex function.
At this point I have made a fairly permanent switch from evolutionary methods to reinforcement learning methods. I have written a good chunk of code so far to begin testing new ideas, including the basic neural network setup, temporal difference learning, and back-propagation. The back-prop will probably be used by the "sensory predictor" (i.e. internal/world model) to learn an internal representation of the external environment. Back-prop seems to be good for this because there will be predicted sensory inputs and actual sensory inputs, naturally leading to error signals at each output neuron.
I have run a few simple tests to make sure each component is functioning properly. The thing I'm testing now is a simple classical conditioning response. I'm trying to get my new agents to be able to predict rewards given some stimulus 200 ms before reward reception.
In the future I would like to setup a SETI-like system for training simulated creatures and/or robots. I think it would be a good way to get people involved in AI research, not to mention the extra CPU resources.
Right now I'm preparing a Verve presentation for the ISU Robotics Club tomorrow which will basically cover everything in this post, plus a little more background information. I'm hoping to use Verve to train real robots in the future (as opposed to simulated creatures). Maybe some folks from the club will be interested in working on something like that.
Tyler
Subscribe to:
Comments (Atom)