One more value function image...

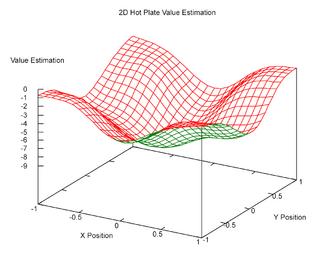
Here's another version of the estimated value function for the agent in the 2D world described in the previous post. This was generated as a scalable vector graphics from from gnuplot, and I converted it to a PNG:

Simple value function images

Here are a couple of sample (estimated) value functions, both using radial basis functions for state representation.

The first one is for an agent in a 1D world with -1 reward everywhere except on the left and right side:


This second one is for an agent in a 2D world with -1 reward everywhere except at the 4 corners:

State representation update

I've been working on writing my master's thesis lately. I'm trying to finish it by Nov. 1st. I'll post a link to it when I'm done. I also plan on overhauling the Verve website before too long... at least by the time I release an initial version.

Here's a quick summary of my recent thoughts on state representation:

• The agent should have a linear state representation in order to assure temporal difference learning convergence. We need to transform the direct sensory inputs into this linear form.
• The state representation should contain features that combine certain inputs where necessary. For a general purpose agent we need to use features that encompass all possible combinations of sensory inputs. Over time the features that never get used could be purged.
• The boxes approach, tile coding, radial basis functions, etc. are all valid methods we could use to represent these features in a linear form. For now I'm choosing an RBF state representation that combines all inputs. Later I would like to experiment with hierarchies of RBF arrays to mimic the hierarchical sensory processing in the cortex.
• We could reduce the dimensionality of sensory inputs by using principal components analysis (PCA) or independent components analysis (ICA). I considered trying this, but I won't have time before finishing my thesis. I might use the "candid covariance-free incremental principal component analysis" (CCIPCA) method since it's incremental and seems fast.

The last thing I want to implement for my thesis is planning. The following is the general design described using the boxes approach. (Things get a little more complicated now that we're using RBFs, described later.) I would have a state-action array of boxes with a single active box representing a unique state-action combination. This array would connect to another array representing the predicted next state and a single predicted reward element. This state/reward predictor would be trained with a simple delta rule using the actual state and reward. The predicted state array would use a winner-take-all rule to pick the predicted next state. Since the winner-take-all system uses roulette selection with selection probabilities for each state, we can interpret these probabilities as the agent's prediction certainty. These certainty/uncertainty values can be used to generate curiosity rewards (proportional to uncertainty); agents are attracted to uncertain situations until they learn to predict them, at which point they get bored. Using the state/reward predictor, the agent can shut off its actual sensory inputs and run "simulated experiences" using this predictive model. It uses this system to learn its value function and policy without having to interact with the environment constantly.

The main changes when replacing the boxes with RBFs are the following: Instead of using a state-action array of boxes, we need an "observation"-action array of RBFs. Here we are taking the actual sensory input (i.e. the observation) combined with a particular action and transforming them into an RBF representation. This RBF array projects to a predicted observation and reward array of neurons. The system is still trained using a delta rule. The observation/reward predictor no longer uses a winner-take-all rule: instead of choosing a single next state, we have an array of real-valued outputs representing the predicted next observation (and reward).

More to come when I get further...