I Need a Better State Representation

I'm trying to come up with a better way to represent the current state. Right now I use the "boxes" approach, as described in the last post. Another idea is "tile coding" (aka CMAC) described in Sutton & Barto's RL book. I think the boxes method is like having a single tiling, but in general you could have any number of tilings, each offset a little from the others. That means that with 5 tilings over some input space, you would have 5 active tiles, one from each tiling. Tile coding would give better generalization than using the simple boxes approach. Also, there are ways to use hashing to reduce the memory needed; memory would only be allocated when new states are encountered.

It would be nice to have an array of states where only the "important" states are represented. This could even be dynamic where newly encountered states are compared to the existing list of states. If a new state is different enough, it would be added to the list.

There are a lot of things I could try, but I want to finish adding new features and testing before October, then write my thesis in November. So if I'm going to improve the state representation, I don't want to have to try anything too experimental.

Solved Pendulum Task (and others)

I finally solved the pendulum swing-up task the other day. Here's a picture of it balancing itself:



The main change that helped solve this task was the following relatively major change: I no longer use radial basis functions. Instead, I discretize all incoming continuous inputs into separate "boxes" (to use the terminology from the literature) and generate a list of all possible combinations of the input signals. So in the case of the pendulum, say we discretize the two inputs (pendulum angle and angular velocity) into 12 boxes each. That means the intermediate state representation is an array of 144 possible combinations, each one representing a unique state. It's kind of a brute-force method, but it's very reliable and easy to understand. I may come back to radial basis functions and hebbian learning mechanisms later to form a more compact state representation.

Here are some pictures of the pendulum's (simple) neural network before and after learning the task. Excitatory connections are green, inhibitory are red. The connection diameter represents its weight's magnitude.



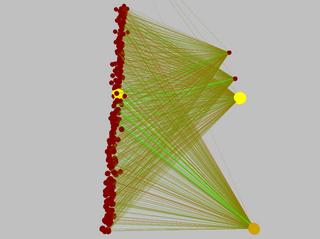
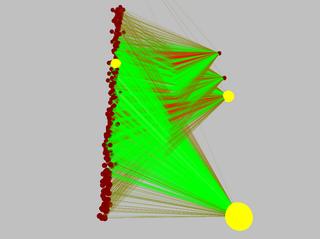
So here's a list of the tasks solved so far (with the number of inputs and outputs specified as (inputs/outputs)):
- N-armed bandit (0/10)
- hot plate (1/3)
- signaled hot plate (2/3)
- 2D signaled hot plate (3/5)
- pendulum swing up (2/3)

Next up: the inverted pendulum (aka cart-pole)...

One more thing: I used SWIG to generate Python bindings. Verve seems to work pretty well as a Python module. I don't know if I'll use it much right away, but it's good to have around.