Self-Organizing RBF Methods

Lately I've been thinking about various methods for self-organizing RBF centers. Instead of having RBF position fixed, they could move around over time using an unsupervised learning approach. This would focus resources on the most important parts of the input space.

Below I described a few different adaptation methods. "x" represents the distance between an RBF and the input point. I tested some of these ideas in a simple PyGame application and posted some screenshots below.

Method 1
Move the RBF closer to the input point in proportion to x. The farther away the RBF is from the input point, the faster it will move towards it. In other words, given input that stays in the same place over time, all the RBFs will reach it at the same time.

This method can be made more local by only considering RBFs within some radius from the input. The following image shows units being adapted towards the mouse pointer in my PyGame app. Adaptation is proportional to x.



You can see how all of the units beyond a certain radius do not move at all.

Method 2
If we adapt the RBF positions based on a Gaussian function...



...the RBFs will move towards the input point faster as they approach it. This is desirable because more distant points will not be affected as much. The following screenshot from my PyGame application demonstrates this using a Gaussian-based adaptation function. I moved the mouse pointer (which determines the input point) around in a smooth curve.



The problem with these approaches is that the RBFs tend to clump together near the inputs... which is fine if your goal is to reach a set of discrete clusters, but not if you're trying to approximate some function. In my case, I'm usually trying to represent a state space for a physically-simulated creature, so I don't want the RBFs to clump together so much. I do want them to move towards the input points (presumably increasing the representation's resolution where it matters), but not so much that they're totally covering the exact same area.

Method 3
I tried a hybrid approach which combines the simple linear function of Method 1 and the Gaussian function of Method 2. By simply multiplying the Gaussian and linear functions, I got the following:




This looks like it would help because the RBFs adapt slowly at large distances, quickly at medium distances, then slow down again as they approach the input. This is, in fact, what it does, but I still get the clumping effect I was trying to avoid. The following picture shows the PyGame app using this hybrid approach. It's hard to tell the difference between this and the plain Gaussian method just by looking at the picture; the main difference is in how quickly the RBFs approach the input.





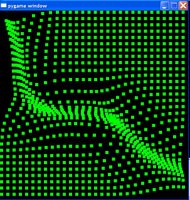
So now I have a few methods to self-adapt RBF centers. (Of course, these have probably already been described elsewhere, but sometimes it's fun and enlightening to figure these things out yourself.)

The problem remains that the RBFs clump too much. What I need is a good way to keep them a minimum distance apart. A brute-force approach would be to compute the distances between each pair of RBFs, but that's O(n^2) runtime complexity. The classic Kohonen's self-organizing map approach would probably work. To implement that I would simply need to add connections between nearby RBFs, and I could use those local connections to force them apart if they get too close.

GDC 2006 Summary

This is a summary of my GDC 2006 experience. Keep in mind that I attended only ~15 out the the several hundred lectures available, and most of the ones I attended were in the programming track.

Overall
GDC 2006 was a continuation of last year's topics. Compared to last year, there was nothing terribly revolutionary (which was to be expected... there's already enough for people to learn without having to worry about, say, yet another hardware platform). With all the new hardware coming out, most of the focus was on preparing developers for the transition to parallel processing. Overall, it was a great conference; I think the GDC is one of the most important conferences available for people interested in real time computer graphics, simulated physics, AI, software development techniques, 3D modeling, etc.

In the game programming world, there was more of a push towards parallel architectures and algorithms. This change started last year with the introduction of new hardware (the Cell chip for the PS3, Ageia's PhysX chip, and multiple core chips for PCs).

Sessions
I attended the following sessions. For some of these I was working as a conference associate; the rest I attended for my own interest. More info on these can be found on the GDC 2006 site.

• A day long tutorial, "Embodied Agents in Computer Games," by John O'Brien and Bryan Stout.
• A roundtable discussion, "Technical Issues in Tools Development," moderated by John Walker.
• A keynote speech, "Building a Better Battlestar," by Ronald D. Moore.
• "The Next Generation Animation Panel," by Okan Arikan, Leslie Ikemoto, Lucas Kovar, Julien Merceron, Ken Perlin, and Victor Zordan.
• "High Performance Physics Solver Design for Next Generation Consoles," by Vangelis Kokkevis. This included a demo of 500,000 particles running in real time on the PS3.
• "Sim, Render, Repeat - An Analysis of Game Loop Architectures," by Michael Balfour and Daniel Martin.
• The Nintendo keynote speech, "Disrupting Development," by Satoru Iwata. They handed out several thousand free copies of Brain Age for the Nintendo DS.
• "Serious Games Catch-Up," by Ben Sawyer.
• "The Game Design Challenge: The Nobel Peace Prize," by Cliff Bleszinski, Harvey Smith, Keita Takahashi, and Eric Zimmerman.
• "Spore: Preproduction Through Prototyping," by Eric Todd.
• "Half Weasel, Half Otter, All Trouble: A Postmortem of Daxter for the Sony PSP," by Didier Malenfant.
• "Physical Gameplay in Half-Life 2," by Jay Stelly.
• "Behavioral Animation for Next-Generation Characters" (Havok sponsored session), by Jeff Yates.
• "Crowd Simulation on PS3," by Craig Reynolds. Showed 10,000 fish interacting @60 fps on the PS3.
  

People
I made a few new connections this year. I talked to Steve Wozniak, Dan Goodman (who works with Kevin Meinert, a former VRAC researcher, at Lucasarts), Leslie Ikemoto, and a bunch of people from the conference associates group. I also talked with several people that I have met before, including John Walker (High Voltage Software), Mat Best (Natural Motion), and Ken Stanley.

Meeting with Leslie Ikemoto at GDC 2006

At the GDC last week I met Leslie Ikemoto at a tutorial on embodied agents in video games. She brought up the Nero game during the tutorial, which uses evolved neural networks (specifically, the NEAT algorithm, invented by Ken Stanley) to control soldiers in a real-time strategy game. Since I had used NEAT before and am familiar with Ken Stanley and NEAT, I talked to her briefly during a break.

The next day we talked again about our own research. She showed me a project where she trained an animated character to run around on a platform, seeking goals and avoiding barriers, using reinforcement learning. The character's trajectory was determined by the animation sequence, so the RL part learned to choose the best animation to perform at any given state. Overall, it worked pretty well. She was a little unhappy with the results when the character seemed to wander around idly, even though there was a clear path to the goal. My best guess was that the state space needed higher resolution. I also suggested using a clustering algorithm to group the sensors into the most important parts of the state space.

It was very cool to see RL applied to character animation like this. I think it is a very powerful approach, especially in situations where the character must adapt to changing environments. Hopefully we'll see more of this in the future.

Leslie's colleague, Okan Arikan, whom I also met at the GDC, has done some pretty cool computer graphics research. Check out these explosions!

How Much of the Brain is Understood?

A few days ago, right after talking to Steve Wozniak, my friend Ken Kopecky and I were talking about how much of the brain is understood. He asked me roughly how much of it I thought I understood (which is sort of an ill-posed question, but anyway...), and I said maybe 50%. He replied, "That's a very bold statement, Tyler Streeter." I said, "Ya, I know."

The next day I thought more about that conversation. I realized that I should have qualified my response a bit. I talked to Ken again, saying that I was mainly referring to the brain's functional/computational aspects. I said, "My 50% estimation from the other day was not meant to imply that I am especially intelligent, but that the functional, computational aspects of the brain are not as complex as most people think."

To elaborate a bit, some of the key elements (also described in my notes posted earlier) are probably:
* Data compression/feature extraction (e.g., principal components analysis, clustering)
* Reinforcement learning (e.g., temporal difference learning)
* Planning/imagining (e.g., using a learned predictive model of the world to enable reinforcement learning from simulated experiences)
* Curiosity rewards (e.g., intrinsic rewards from novel, learnable information)
* Temporal processing/short-term memory (e.g., tapped delay lines)

Meeting Steve Wozniak at GDC2006

I met Steve Wozniak (cofounder of Apple) today at GDC2006. I showed him some videos of my research, which he enjoyed. He was very eager to meet all of the Conference Associates (the volunteer group of which I am a member).

We talked briefly about the brain and what we currently understand about it. We disagreed about how much is known about the brain. It was a good time.

My Notes on Theoretical and Biological Intelligence

Over the past year I've been keeping a couple of text files that summarize what I know about biological intelligence (from a neuroscience perspective) and theoretical models of intelligence. I am constantly updating these files as I gain more knowledge. I thought it would be good to post them here, just to have a record of what I understood on March 17, 2006.

biological_intelligence_3-17-06.pdf
theoretical_intelligence_3-17-06.pdf

What Does the Cerebellum Do?

The cerebellum automates motor tasks. It learns the temporal relationships between sensory and motor signals. After much practice, motor tasks get transferred to the cerebellum. In other words, well-learned tasks get chunked together as motor programs in the cerebellum. More specifically, these are probably closed-loop policies/options, as defined in the reinforcement learning literature. This whole process frees other areas (in the cerebral cortex) to focus its attention on new tasks, building upon the automatic skills stored in the cerebellum. It enables agents to learn hierarchies of motor skills.

Functions of Predictive Models

What are predictive models good for? Here's what I think:

• Planning - Without an accurate predictive model, it's impossible to generate simulated experiences. Planning requires a predictive model.
  
• Curiosity - The only models of curiosity I've seen so far depend upon prediction. Curiosity is defined as novelty or, even better, the reduction in novelty over time. The only good way to measure novelty in a general way is by comparing the output of a predictive model with reality. This could include a reflexive, metapredictor component that can predict a level of uncertainty about its own predictions.
  
• Attention - I think attention is drawn to unpredicted, novel situations (and novelty measurement depends upon predictive models... see Curiosity above). In other words, the limited attention channel is focused on situations that contain the highest probability of containing useful information. These can be externally driven (unpredicted external stimuli) or internally driven (through planning/simulated experiences, we might come to a novel situation which attracts our attention and may guide external movement toward that situation in the real world).
  

Note that, in any kind of general purpose intelligent agent, predictive models must be learned from experience.